Bell's Inequalities Revisited

Last Update November 22 2022

Abstract

Quantum mechanics statistics, no matter how spectacular, do not mandate uncertainty. Proof is a simple equation based on a hidden variable just as predicted by EPR.
In the following classical physics is also referred to as local reality; by contrast non-locality characterizes Quantum Mechanics.
Beware the following so-called local reality interpretation, because contradicting non-locality, is simply abnegated by most physicists nowadays.

1. Introduction

A pair of entangled particles is made of 2 complementary particles emitted at same time by one emitter in two opposite directions, and analyzed within two receivers equidistant from the emitter.
There are two schools of thoughts concerning the measures of entangled pairs:

1. Along Bohr's thinking is Quantum Mechanics in which statistics, called probabilities in the litterature, and uncertainty rule. Uncertainty rules because entangled pairs, at time of emission, are all identical to each other; no matter where, no matter when emitted all entangled pairs have and will be occurring under a unique and identical quantum state made of eight simultaneous yet incompatible constitutions. When a particle of any pair is measured one of these eight outcomes haphazardly pops out; and the measured particle is instantaneously instructing over distance the companion particle to comply, a phenomenon known as non-locality; at that very time the pair's quantum state and its uncertainty vanish.
2. Along Einstein, Podolsky, Rosen or EPR paper [Ref. 1] published in 1935 is conventional physics, or local realism, which asserts that behind quantum statistics and uncertainty are hidden variables; without questioning Quantum mathematics and statistical results EPR nevertheless challenges both uncertainty and nonlocality mental concepts attached to it.

Later in 1964, well after above controversy was mathematically confirmed and before any experiments were run, John Stewart Bell came up with his famous inequalities [Ref. 2], establishing that should future physical experiments justify Quantum Mechanics, as summarized in section 1 above, there would be no hidden variables and no Classical or local theory would ever be established.

In the 1980s physical experiments run by Alain Aspect [Ref. 3], and many others since, have definitely justified quantum statistics predictions.
Since then the consensus in science is that there is no hidden variable, Einstein equation is dismissed, and no local theory will ever be established.
Science physics and mathematics loses some of its prestige as two valid mathematical theories, EPR and Bell's inequalities, are contradicting each other.
This page restores Science's great stature, it demonstrates that Einstein, Podolsky and Rosen are right, without negating Quantum Statistical mathematics; the physical results can be justified using local reality, showing non locality is not mandated by statistics.

2. Conventions and the Mathematical Discord

The following interpretation is occurring in local reality classical physics.
Beware, in quantum Mechanics the orientations of the particles are non-existent until the measurements occur; and that is so primordial to most physicists that some told me the following is irrelevant and is not to be considered.

2.1 Conventions

In order to describe the situation some conventions are needed. In the following the trigonometric notation is used; the 0⁰ angular reference coincides to the entangled pairs trajectory also equal to 360⁰; and by definition positive angles are counted counter clockwise.
While entangled pairs are either two photons or two electrons particles in Quantum Mechanics, for simplicity this non-quantum or local interpretation deals with electrons only.

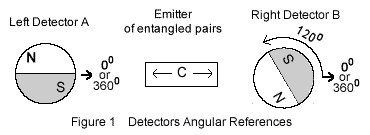
2.2 Detectors orientations

In this local reality interpretation, the entangled electrons are measured by 2 detectors (called polarizers in science), each being given an orientation by the experimenters.
Figure 1 illustrates the physical experiments. It consists of two detectors' magnets A and B on either side of an emitter C of entangled pairs of electrons. The detectors magnets are graphically represented by a circumference and a diameter line delineating the North Pole, labeled with a capital "N", from the South Pole "S" represented in grey. In Figure 1 detector A is oriented at 0⁰ while detector B is oriented at 120⁰.
Important note: in Quantum Mechanics' non-locality, the detectors just as in local reality are physically oriented too.
It turns out that these two specific orientations, and more specifically the difference 120 degrees between the two detectors is, as explained below, at the base of the controversy.

2.3 The two electron's magnetic orientations or tilts of any individual pair are opposite

Once more the following does not exist or is forbidden in quantum physics.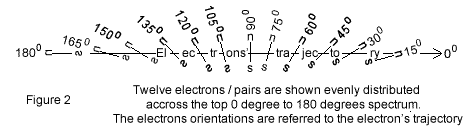
In local reality an electron is made of a rotating electric charge acting as a magnet, which north pole is defined with the right hand rule; curving the right fingers along the electron's spin, the thumb points north, which defines the magnetic direction of the electron called tilt in this web page; here an electron is represented with a bar and two small "s" and "n" letters for their south and north poles.
Figure 2 represents 12 electrons, whose angular tilts are represented counter clockwise with respect to their trajectory.
In this local reality interpretation each electron's tilt is specifically determined.
In contradiction Quantum mechanics asserts that the electrons have no magnetic orientation at all; all pairs share an identical and unique quantum state, which implicates uncertainty, and which defies human brains whether scientific or not.

2.4 Green versus Red measures

In this local interpretation each electron magnetic orientation of each entangled pair is confronted to its detector and individually measured.
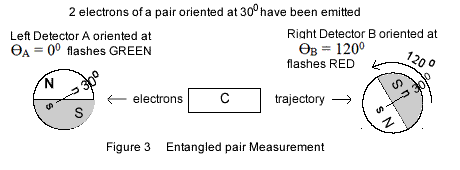
In Figure 3 the angles ΘA and ΘB (read theta) are the orientations respectively given to Detector A and Detector B magnets.
Figure 3 illustrates the measurement of a single entangled pair emitted with a 30⁰ magnetic tilt; the 2 electrons are represented within their respective Detectors A and B.
If the electron north pole matches detector North Pole, the detector flashes GREEN (or G) as Detector A does. When they do not match, they flash RED (R) as Detector B does.
Note that entangled pairs are made of 2 complementary particles, meaning their tilts are 180 degrees apart. For easier presentation and comprehension, the graphs and this text are handling pairs having identical tilts instead. I found out that pairs with identical tilts are providing as good results as complementary pairs even though forbidden in quantum theory.
Please note also, in quantum mechanics, the complementary appellation excludes angular values, keeping it purposely undefined.

2.5 Bell's theorem local interpretation

Before any experiments could be run the following was asserted. Electron's tilted between 0⁰ and 120⁰ represent two thirds of those tilted within the upper 0⁰ to 180⁰ half circle; according to Figure 3 they will flash RED in detector B and GREEN in detector A; the remaining pairs tilted between 120⁰ and 180⁰, or one third of the upper half circle will flash GREEN in both detectors. The conditions below the electrons' trajectory from 180⁰ to 360⁰ being symmetrical to those above the electrons' trajectory, the same one third two thirds distribution applies.
And no matter the number of pairs considered, this reasoning applies.

When the detectors angles are ΘA = 0⁰ and ΘB = 120⁰, as in Figure 3, this local interpretation provides one third same colors to two thirds different colors distribution.

2.6 Quantum Mechanics predictions

Mermin [Ref. 4] provides Quantum Mechanics equation, which was also established before any experiments took place:

The detectors orientations Θ_A and Θ_B can be each given any values from 0⁰ to 360⁰. Quantum Mechanics Equation 1 provides the following same colors to different colors ratio.

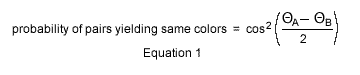
When the detectors angles are ΘA = 0⁰ and ΘB = 120⁰, as in Figure 3, this equation predicts that same colors (either GG or RR) will be flashed one-quarter of the times, and opposite colors (either RG or GR) will be flashed three-quarters of the time.

2.7 Science's stunning mathematical discord

The physical experiments and resulting measures, which occurred later, precisely matched Equation 1 results.
This situation, in which one third two thirds local reality allegedly undeniable distribution contradicts the one quarter three quarters distribution predicted by Quantum Mechanics and finally found to comply with experiments, is stunning and remained as such until following Equation 2 appeared.

3. Local Mathematics Conforming to Experiments

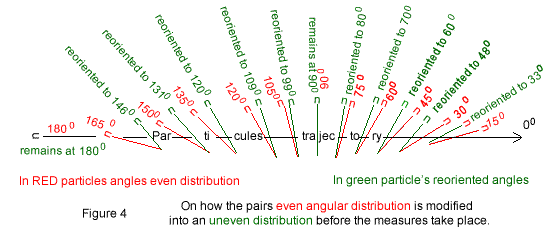
Once more beware, the following is simply denied by Quantum Mechanics' non-locality advocates.
Provided the pairs are evenly distributed, those with tilts between 0⁰ and 135⁰ represent three quarters of those above the electron's trajectory. The remaining pairs between 135⁰ and 180⁰ make the remaining quarter. And an identical distribution applies to the circle's lower half.
In order to match the physical measures and Quantum Mechanics statistics when the detectors are set 120⁰ apart, it suffices to come up with an equation that modifies the pairs tilted between 0⁰ and 135⁰ labelled evenly distributed to angles tilted between 0⁰ and 120⁰ now renamed reoriented. The pairs evenly distributed between 0⁰ and 180⁰ are reoriented from Θ_{electron evenly distributed} to Θ_{electron reoriented} as follows:

When the detectors are oriented 120⁰ apart as in Figure 3, the electrons evenly tilted from 0⁰ to 135⁰ (Θ_{electron evenly distributed}) when emitted will be reoriented and measured by Detector B between 0⁰ and 120⁰ (Θ_{electron reoriented}) just as the measures show and just as predicted by Quantum Statistics.
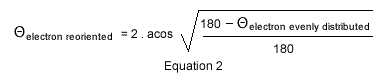
Note, the origin chosen to refer to the detectors, as well as the origin chosen to refer to the electrons orientations, when making the measures, are both irrelevant.
Figure 4 illustrates Equation 2; Equation 2 predicts the behavior of each electron of each pair; while agreeing with or conforming to Quantum statistics, equation 2 is nevertheless dethroning the concept of uncertainty.

The red and green lines and angles in Figure 4 represent individual electrons orientations and reorientations of any pair before the measures take place.
In this interpretation the 2 electrons of any pair are acting in concert, not because one particle is instructing instantly over distance the other to comply (Quantum Mechanics nonlocality interpretation), but because, before the measures take place, their individual yet common tilts have each been individually re-oriented by their own specific detector in an amount as provided by Equation 2.
And the 120⁰ difference of orientation between the detectors as used in all of above, is not restrictive; the 2 detectors can be set apart at any other difference than 120⁰; in all cases Equation 2 provides reoriented values that fit the experiments.
Yet as already mentioned the 120 degrees difference is the situation in which the local to non local so called controversy is most evident.
Equation 2 abolishes the former local one third two thirds distribution not conforming to reality in favor of one quarter three quarters distribution conforming to reality.

4 Local reality: the details

Whereas Quantum Mechanics provides the correct distribution of the measures through a single calculation using Equation 1, Equation 2 requires 5 mathematical operations to find out the reorientation of a single electron; and these five operations have to be repeated a great number of times on a great number of pairs to verify the results provided by Equation 2 agree with Quantum Mechanics Equation 1 statistics.
A computer simulation is of the essence; one has been set; click:

Entanglement Computer Simulation.

This simulation illustrates both 25% and 33% distributions using the angular orientation of each particle at emission. The development of the computer simulation revealed that in local-reality the following processes are taking place sequentially in time.
Adopting the trajectory of the entangled pairs for angular reference here is what is happening:

1. To start with, the two electrons of any entangled pair are emitted having opposite orientations.
   Please recall, this angular relation between the 2 electrons at emission is not part of Quantum Mechanics; the claim made in Quantum Mechanics is that the particles have no specific angular orientations until the measures occur, at which time the uncertainty disappears, their orientations appear providing the measured results.
   
2. Within its own detector each electron is individually diffracted; that is, its angular orientation is deviated by an angle provided by local Equation 2.

The RIGHT measure is related to the LEFT, for each pair, in 2 different ways: the 2 electrons of each pair are emitted having opposite orientations; the 2 detectors are set 120 degrees apart; both factors remaining correlative throughout the experiment no matter the distance separating the 2 detectors.
Please take note that nothing is happening until the measures are taking place; showing that quantum mechanics argument, namely that everything is happening at time of measure, cannot be used to justify non-locality.

A few conditions must be in effect in order to obtain both wrong and correct statistics coinciding with Bell's inequalities; the pairs have to be evenly distributed across the entire 360 degrees sector. And to comply exactly with both one third , one quarter distributions the number of pairs emitted must be an entire number of quarters and thirds at same time; for instance emitting a total of 12 or 24 or 360 pairs, which are numbers evenly divided by 3 and by 4, are acceptable.
Local equation 2 simply nullifies the wrong local reality, which is used in Bell's inequalities and which by the way is also recognized as being wrong in Quantum Mechanics; most importantly EPR is now justified.

Note regarding the computer simulation that I designed and I am proposing
I have been told this Entanglement Computer Simulation I wrote is concerning a specific case, and not the general phenomenon and as such is irrelevant.
My answer is that my program precisely simulates the Alain Aspect experiment, which is the quintessential case on which all of Quantum Mechanics sprouted up.
The fact of the matter is any computer simulation based on Quantum Mechanics Equation 1 probabilities will never provide the individual measures obtained physically in the experiments. By contrast this Simulation based on Equation 2 does; it provides the details of Mother Nature beautiful, precise, yet sly behavior.

Note about science's entangled pair complementarity
In science the pairs make one complementary entity until measured, the word complementary specifically excluding any physical characteristics. In quantum mechanics the 2 electrons of any pair, until measured, are not distinguishable, and more specifically devoid of any angular orientation; even though the emitting of any pair, that is science's physical emission process, specifically suggests that the 2 particles' orientations are at 180 degrees from each other.
Contrary to quantum science I am using entangled pairs occurring as 2 individual particles; the 2 particles having either opposite or identical magnetic orientations that I call tilts; the pairs' tilts differing from pair to pair.
My computer simulation showed that both cases, identical orientations and opposite (180 degrees) orientations within pairs provide the correct answers, even though pairs of identical particles (opposite of complementary) are forbidden in quantum mechanics.
When the pairs have identical tilts, 25 percent of them flash the same color 75 percent flash differing colors; when the 2 particles are oriented 180 degrees apart (coinciding to quantum mechanics complementary definition) 75 percent of them instead flash the same color, 25 percent flash differing colors; the quantum ratio one quarter, three quarters departing from one third two thirds remaining nevertheless in force in both complementary and non-complementary situations.
Such distinctions are apparently kept hidden in physical experiments.

5. What about unification ...

For a while the one-third wrong distribution has been justified using three overlapping circles as explained in details on 'YouTube' Reference 5 below. Yet while the local-reality interpretation introduced here shows that such justification does not take into account the phenomenon of diffraction, those who defend non-locality argue that their reasoning or their logic is nevertheless right and as such this local reality interpretation remains irrelevant.

So I dug deeper and looked in more detail at Bell's inequalities in order to come up with an argument that can no longer be denied by those believing in non-locality; that is an argument that does not disprove Quantum Mechanics fundamentals.
In Wikipedia's page labeled 'Bell's theorem' [Ref. 6] is the following:
"However, Bell discovered something new by rephrasing the problem as two alternatives. Either quantum mechanics is correct because quantum entanglement exists, or quantum mechanics is incorrect because quantum entanglement does not exist. Bell showed that any hidden variable theory would be subject to certain constraints, including the necessity of quantum entanglement."

Now that is a whole new ballgame! Now local-reality may include a quantum entanglement allowing for conciliation; evidently the question becomes: is there any quantum entanglement in local reality?
And to answer that question I had to find out what is meant by quantum entanglement
I found an explanation through another Wikipedia article conveniently labeled Quantum Entanglement Reference 7 below, and which reads as follows:
"Quantum entanglement is a label for the observed physical phenomenon that occurs when a pair or group of particles is generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the pair or group cannot be described independently of the state of the others, even when the particles are separated by a large distance."

Recalling section 'A' above, which states that the 2 particles of any entangled pair are generated having opposite directions, a feast by the way that requires specific emissions processes using specific atoms, any particle of any entangled pair in local-reality, just as in Quantum Mechanics, "cannot be described independently of the state of the other even when the particles are separated by a large distance".
Entangled pairs are emitted as 2 particles of opposite directions. The point is that these 2 opposite directions for each pair remain in effect no matter the distance up to their measures; and that abolishes the instant communication between the 2 particles, which in Quantum Mechanics is required to provide the final results.
Furthermore Quantum mechanics 25% prediction relies on the fact that the 2 detectors are oriented at 120 degrees from each other ; that is another 2 individual parameters, which can be separated by huge distances yet acting in concern that is acting in a quantum entanglement manner.
These specific, within pairs orientations and detectors orientations, are implementing this so-called quantum state whether it be local reality or Quantum Mechanics.
The irony is that quantum-entanglement is not the only reason behind the controversy; another imperative factor, behind the measures, is the diffraction phenomenon overlooked in science.

6. Conclusion

This web-page's ultimate goal is to refute both uncertainty and non-locality concepts. Showing that both concepts are not mandated by Quantum Mechanics predictions. This goal is achieved with a local equation, which fits Quantum Mechanics statistical interpretation.
Another goal is to provide as best as possible a physical explanation of the phenomenon as done in section 4 above.

Statistics does not mandate uncertainty
Both Quantum Equation 1 and local Equation 2 are correctly cloning reality. Showing that Equation 1 does not mandate uncertainty.

Nonlocality is unreasonably commended
When the detectors are set 120⁰ apart, a pair emitted at 30⁰, as shown in Figure 3, is measured GREEN by one detector and RED by the other; all in all the two electrons of a pair may be measured differently. Yet such measures, when the two colors measured do not comply, were witnessed by human operators even before Equation 2 came into play.
Nonlocality, which states that when one electron is measured the other complies at distance, then cannot refer to the colors measured. Nonlocality must then refer to the fact that quantum statistics, which are correct, do not coincide to the expected local (and wrong) outcome used by Bell; non locality is a byproduct of unexplained statistics and vanishes with Equation 2.

Bell's inequalities revisited
In the end Bell's famous theorem leads toward conciliation as shown in section 5 above.

Whatever EPR's hidden variables are, they are
This interpretation has the definite advantage to confirm that Einstein and colleagues' mathematics is right after all. The hidden variable is evidently the particle's individual orientation.

References

[1] Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete?
Phys. Rev. 47, 777-780 (1935).
Also available on the internet at: EPR
[2] Bell, J.S.: On the Einstein Podolsky Rosen paradox. Phys. 1, 195-200 (1964)
Available on internet at: Bell's inequalities
[2 a] For everybody explanation: Bell's inequalities for everybody
[3] Aspect, A., Grangier, P., Roger, G.: Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedanken experiment: a new violation of Bell's inequalities. Phys. Rev. Lett. 49, 91-94 (1982) Available on Internet: Alain Aspect experiments
[4] American Journal Of Physics; Volume 49; Number 10; Page 940; October 1981.
Bringing home the atomic world: Quantum mysteries for anybody. By N.D.Mermin.
Also available on internet: Mermin's paper
[5] See On how the 33% distribution is set ignoring the particles orientations
[6] Quote found Dec 19 2019 on Wikipedia at Wikipedia, the free encyclopedia title: Bell's theorem
[7] Quote also found Dec 19 2019 on Wikipedia at Wikipedia, the free encyclopedia title: Quantum entanglement

Appendix A: Quantum Mechanics hidden side

This section sheds light on Quantum Mechanics Equation 1 extraordinary alchemy.
As noted in "3. Local Mathematics Conforming to Experiment" the origin chosen to refer to the detectors' orientations is irrelevant. We can then choose Detector B as being the reference in Equation 1, which can then be rewritten as:

Both Equation 1 and its hidden aspect deal with the detectors' orientations rather than with the electrons tilts as does Equation2; the hidden side of Equation 1 suggests that detectors' orientations just as electrons' tilts can be re-oriented in order to describe the entanglement phenomenon. Equation 3, which is inspired by above hidden aspect of Equation 1, does just that:

Equation 3 modifies θ_{DetectorNominalOrientation} = 120⁰ into θ_{DetectorEffectiveOrientation} = 135⁰ and θ_{DetectorNominalOrientation} = 0⁰ remains unchanged at θ_{DetectorEffectiveOrientation} = 0⁰.
In these conditions one quarter identical measures instead of one third identical measures will occur, provided the emitted electrons are evenly distributed over the full 360⁰ circumference.
In the end Quantum Mechanics extraordinary alchemy mends nicely with local reality.

Contact:   henriJMsalles[at]gmail.com
Copyright © by Henri Salles. You have the permission to reproduce, print, distribute and post the contents of this webpage, provided you mention proper citation and acknowledgment: www.bell-s-inequalities-revisited.com
or the link: https://bell-s-inequalities-revisited.com by Henri Salles